
문제 설명
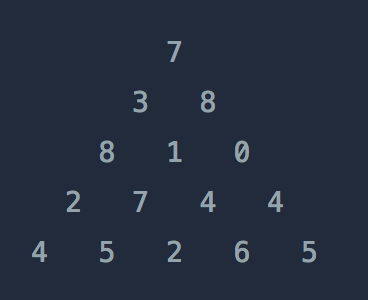
위와 같은 삼각형의 꼭대기에서 바닥까지 이어지는 경로 중, 거쳐간 숫자의 합이 가장 큰 경우를 찾아보려고 합니다. 아래 칸으로 이동할 때는 대각선 방향으로 한 칸 오른쪽 또는 왼쪽으로만 이동 가능합니다. 예를 들어 3에서는 그 아래칸의 8 또는 1로만 이동이 가능합니다.
삼각형의 정보가 담긴 배열 triangle이 매개변수로 주어질 때, 거쳐간 숫자의 최댓값을 return 하도록 solution 함수를 완성하세요.
제한사항
- 삼각형의 높이는 1 이상 500 이하입니다.
- 삼각형을 이루고 있는 숫자는 0 이상 9,999 이하의 정수입니다.
입출력 예
triangleresult
| [[7], [3, 8], [8, 1, 0], [2, 7, 4, 4], [4, 5, 2, 6, 5]] | 30 |
Sweden
International Olympiad in Informatics – Statistics Contact information Participation in IOI (based on database records) First participation: 1990Years participated: 31Contestants participated: 82 Perfomance in IOI Gold medals: 13Silver medals: 30Bronze m
stats.ioinformatics.org
프로그래머스의 LEVEL 3에 있는 정수 삼각형 문제이다.
문제 설명을 보면 Dynamic Programming 개념을 통해서 풀라고 나와있다.
나는 동적 프로그래밍이 처음에는 재귀 호출을 통해서 푸는 방식이라고 생각했는데,
이 문제를 보면서 다시 알게 된 것은
재귀호출도 그렇고 이 정수 삼각형 문제도 그렇고
"처음부터 하나씩 쌓아나가는 개념" 이라는 것을 깨달았다.
내가 푼 방식은 for문을 2번 돌리면서 진행하는데,
생각한거와는 다르게 채점 시 Timeout 에러가 발생하지 않았고,
문제에 따라서는 모든 정수에 한번씩은 다 접근해야하는 경우에 이렇게 Dynamic Programming을 통해 풀 수 있는 거 같다.
아래는 내가 푼 코드이다.
def solution(triangle):
for i in range(1,len(triangle)):
for j in range(len(triangle[i])):
if j == 0:
triangle[i][j] += triangle[i-1][0]
elif j == len(triangle[i])-1:
triangle[i][j] += triangle[i-1][j-1]
else:
triangle[i][j] += max(triangle[i-1][j-1],triangle[i-1][j])
return max(triangle[-1])
'프로그래머스' 카테고리의 다른 글
| 프로그래머스 '위장' 문제풀이 - Henry'Algorithm (0) | 2020.10.07 |
|---|---|
| 프로그래머스 '전화번호 목록' 문제풀이 - Henry's Algorithm (0) | 2020.10.07 |
| 프로그래머스 '네트워크' 문제풀이 - Henry'Algorithm (0) | 2020.09.24 |
| 프로그래머스 '124 나라의 숫자' 문제풀이 - Henry'Algorithm (0) | 2020.09.07 |
| 프로그래머스 '체육복' 문제풀이 - Henry'Algorithm (0) | 2020.09.07 |